終価係数などの6つの係数といわれる係数早見表を使用した資金の計算問題は実技試験では毎回必ず出題されています。
過去7回の実技試験ではFP2級で必ず3問、FP3級で必ず1問出題されています。
ただ、この係数の名前が覚えにくいです。
「〇〇終価係数」や「〇〇現価係数」がすべての名前についていればわかりやすいですが、「減債基金係数」や「資本回収係数」など違う名前もあります。
その結果、問題でどの係数を使用すればよいか迷ってしまいます。
そこで、各係数の名前を覚えなくても問題文の「キーワード」からどの係数を使用すればわかる方法を解説します。
ちょっとした【裏ワザ】の求め方もありますので是非活用ください!
1.各係数の基本的な考え方
各係数は複利計算を元にしています。
ただ、6つの係数を使用した問題では複利計算を使わずに答えを出します。
なので、複利=利息と考えて問題ありません。
お金を貯める場合は貯蓄をした金額に利息が付くため貯蓄額より多く貯まります。
貯めたお金を使う場合は使っている間貯蓄した金額に利息が付くため最初の貯蓄額よりも多く使えます。
この多く貯まる、多く使えるという考え方を頭に入れて、それぞの係数を見ていくと理解しやすいと思います。
各係数を見ると1よりも大きい係数になっているものが3つ、1よりも小さい係数になっているものが3つあります。(1年目は除きます)
1よりも大きい係数では1からおまり大きくない係数が1つ、1からだいぶ大きい係数が2つあります。
1よりも小さい係数では1からあまり小さくない係数が1つ、1からだいぶ小さい係数が2つあります。
係数早見表を見た時に1よりも大きいのか小さいのか、1よりもあまり大きくないのか大きいのか、1よりもあまり小さくないのか小さいのかということに注目しましょう。
それでは各係数について簡単に説明していきます。
①終価係数
最初に貯蓄用に用意した金額(元金)が複利でどのくらい増えるかという計算です。
元金に利息が付くので、元金よりも最終的な貯蓄額が多くなります。
問題では元金が設定されるため1倍より大きな係数3つのどれかになります。
終価係数は利息での増加分しかなく大きく増えないため1からおまり大きくない係数が終価係数になります。
②現価係数
目標金額に達するまでに最初にいくら用意するか求める計算です。
最初に用意する金額には利息がついて目標金額に達するので、最初に用意する金額よりも目標金額が大きくなります。
問題では目標金額が設定されるため1倍より少ない係数3つのどれかになります。
利息での増加分しかなく大きく増えないため1からあまり小さくない係数が現価係数になります。
③年金終価係数
毎年積み立てて最終的な金額を求める計算です。
毎年増えていくので毎年積み立てる金額よりも最終金額が大きくなります。
問題では毎年積み立てる金額が設定されるため1倍よりも大きい係数3つのどれかになります。
毎年積み立てるということは利息が付かなくても年数分は増加するため、1からだいぶ大きい係数2つのどちらかになります。
最終的な金額は複利によって毎年利息が増えるため積立金額×年数よりも最終積立額が大きくなります。
2つの係数を見ると年数よりも大きい経数と小さい係数になっています。
積立金額×年数<最終積立額が成り立つということは年数より大きい係数を使用すれば求められるということです。
④減債基金係数
目標金額を貯めるために毎年積み立てる金額を求める計算です。
毎年積み立てていくので目標金額よりも毎年積み立てる金額の方が小さくなります。
問題では目標金額が設定されるため1倍より小さい係数3つのどれかになります。
毎年積み立てるということは最低でも年数分は分割して積み立てるため1からだいぶ小さい係数2つのどちらかになります。
積み立てた金額には複利によって毎年利息が増えるため目標金額÷年数よりも毎年積み立てる金額が小さくなります。
2つの係数の見比べるとわかりますが1÷年数よりも大きい係数と小さい係数になっていると思います。
目標金額÷年数>積立額が成り立つということは1÷年数よりも小さい係数を使用すれば求められるということです。
ここで迷った時の確かめる方法を教えます。
計算した積立額から
積立額×年数<目標金額
となったほうが正解です。
重要なのは積み立てたお金に利息が付いてくるというとことです。
正しい式はこうなります。
(積立額×年数)+毎年の利息=目標金額
なので積立額×年数は目標金額より少なくて良いということです。
⑤資本回収係数
最初に貯蓄用に用意した金額(元金)から毎年もらう金額を求める計算です。
住宅ローンの計算方法でも使用できます。(この場合はもらうではなく支払う)
毎年もらう(支払う)金額を計算するため、元金よりも毎年もらう(支払う)金額が小さくなります。
問題では元金が設定されるため1倍よりも小さい係数3つのどれかになります。
毎年もらう(支払う)ということは最低でも年数分は分割してもらう(支払う)ため1からだいぶ小さい係数2つのどちらかになります。
元金には複利によって毎年利息が増えるため元金÷年数よりも毎年もらう金額が大きくなります。
住宅ローンでは返済の残金に複利が付きます(毎年利息が付きます)のでローン金額÷年数よりも毎年支払う金額が大きくなります。
2つの係数の見比べるとわかりますが1÷年数よりも大きい係数と小さい係数になっていると思います。
元金÷年数<毎年もらう金額が成り立つということは1÷年数よりも大きい係数を使用すれば求められるということです。
ここで迷った時の確かめる方法を教えます。
計算した毎年もらう金額から
毎年もらう金額×年数>元金
となったほうが正解です。
重要なのは残っている元手に利息が付いてくるというとことです。
正しい式はこうなります。
毎年もらう金額×年数=元手+毎年の利息
なので、毎年もらう金額×年数は元金より多くて良いということです。
住宅ローンでは借りた金額よりも多く支払う必要があるということを知っていればわかりやすいですね。
⑥年金現価係数
決まった期間毎年決まった金額をもらうために最初に貯蓄用に用意する金額(元金)を求めるという計算です。
毎年もらう金額を計算するため毎年もらう金額よりも元金が大きくなります。
問題では毎年もらう金額が設定されるため1倍よりも大きい係数3つのどれかになります。
毎年もらうということは最低でも年数分は増加するため1からだいぶ大きい係数2つのどちらかになります。
毎年もらう金額を差し引いた残金は複利によって毎年利息が増えるため毎年もらう金額×年数が元金よりも大きくなります。
2つの係数を見比べるとわかりますが年数よりも大きい経数と小さい係数になっていると思います。
毎年もらう金額×年数>元金が成り立つということは年数よりも小さい係数を使用すれば求められるということです。
2.6つの係数の名前が覚えられない時の解き方
6つの係数の名前は「〇〇終価係数」や「〇〇現価係数」という名前で統一されていれば覚えやすいですが「減債基金係数」や「資本回収係数」のように違う名前のものがあります。
そこで名前を覚えなくでも問題を解く方法を説明していきます。
係数を分類分けする
1%複利の場合の係数早見表は以下のとおりです。
【係数早見表(年利1.0%)】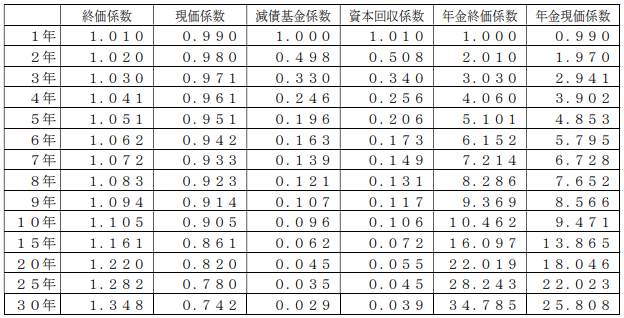
1年目を除くと以下の分類に分けられます。
①1より大きい係数が3つ
これをさらに分解すると以下になります。
・1からおまり大きくない係数が1つ
・1からだいぶ大きい係数が2つ
②1より小さい係数が3つ
これをさらに分解すると以下になります。
・1からあまり小さくない係数が1つ
・1からだいぶ小さい係数が2つ
この4つの分類を係数の名前を使わずに説明していきます。
1よりあまり大きくない係数
1よりあまり大きくない係数を使う時は利息分しか増えない時です。
問題では「〇〇年間、年利1.0%で複利運用した~」という記載があります。
このキーワード以外がない場合にこの係数を使用します。
このキーワード以外とは以下のようなキーワードです。
・〇年間積み立て
・〇年間で切り崩す(ローンの場合は〇年間支払う)
・毎年積立
・毎年受け取る(ローンの場合は毎年支払う)
これらのキーワードがない場合にこの係数を使用します。
1よりあまり小さくない係数
1よりあまり小さくない係数を使う時は目標金額(問題に記載されている金額)に対して必要な金額(答えの金額)から利息分しか増えない時です。
問題では「〇〇年間、年利1.0%で複利運用する~」という記載があります。
このキーワード以外がない場合にこの係数を使用します。
このキーワード以外とは以下のようなキーワードです。
・〇年間積み立て
・〇年間で切り崩す(ローンの場合は〇年間支払う)
・毎年積立
・毎年受け取る(ローンの場合は毎年支払う)
これらのキーワードがない場合にこの係数を使用します。
1よりだいぶ大きい係数(2つ)
1よりだいぶ大きい係数の2つですが係数を見ると以下のような特徴があります。
年数よりも大きい係数と小さい係数
例えば10年目の係数を見てみると以下のような係数です。
10.462 9.471
このとおり10(年目)よりも大きい係数と小さい係数になります。
1年目だけはこの関係が成り立ちませんが問題に1年後は出題されないと思います。(厳密に言うならば年数以上と年数より小さいとすれば1年目もこの関係は成り立ちます)
まず年数より大きい係数についてですが以下のキーワードが出てきた時に使用します。
・〇年間積み立て
・毎年積立
例えば毎年100万円を10年間積み立てたとしましょう。
100万円×10年間=1000万円となります。
ここで問題に必ず記載されているキーワード「年利1.0%で複利運用」が重要になります。
この「年利1.0%で複利運用」という意味は毎年貯まったお金に1.0%の利息が付きますという意味です。
複利の考え方はここでは毎年利息が付くというところが理解できれば問題ありません。
毎年利息が付くということは10年後には1000万円に利息が付いているので1000万円より多くなるということです。
実際に2つの係数で計算してみましょう。
1,000,000×10.462=10,462,000
1,000,000×9.471=9,471,000
1000万円より多くなるので10,462,000が正解となります。
係数だけで判断する場合利息が付くから10倍(年数分)よりも大きい係数を使うということがわかれば2つ計算しなくても答えが出せます。
次に年数より小さい係数についてですが以下のキーワードが出てきた時に使用します。
・〇年間で切り崩す(ローンの場合は〇年間支払う)
・毎年受け取る(ローンの場合は毎年支払う)
この場合問題に記載される金額は切り崩す金額だったり毎年受け取る金額です。
例えば毎年100万円を10年間受取りたいとしましょう。
100万円×10年間=1000万円となります。
ここで問題に必ず記載されているキーワード「年利1.0%で複利運用」が重要になります。
準備したお金は毎年減っていくわけですが残金に利息が付きます。
ということは準備する必要があるお金は以下の関係式が成り立ちます。
準備するお金+残金の利息=1000万円(10年間毎年100万円を受け取る)
よって準備するお金は1000万円より少なくて済むということです。
実際に2つの係数で計算してみましょう。
1,000,000×10.462=10,462,000
1,000,000×9.471=9,471,000
1000万円より少なくて済むので9,471,000が正解となります。
係数だけで判断する場合利息が付くから10倍(年数分)よりも小さい係数を使うということがわかれば2つ計算しなくても答えが出せます。
1よりだいぶ小さい係数(2つ)
1よりだいぶ小さい係数の2つですが係数を見ると以下のような特徴があります。
1÷年数よりも大きい係数と小さい係数
例えば10年目の係数を見てみると以下のような係数です。
0.096 0.106
このとおり10年目(1÷10=0.1)よりも大きい係数と小さい係数になります。
1年目だけはこの関係が成り立ちませんが問題に1年後は出題されないと思います。(厳密に言うならば年数以下と年数より大きいとすれば1年目もこの関係は成り立ちます)
まず1÷年数より小さい係数についてですが以下のキーワードが出てきた時に使用します。
・〇年間積み立て
・毎年積立
例えば1000万円貯めるためにを10年間積み立てたとしましょう。
1000万円÷10年間=100万円となります。
ここで問題に必ず記載されているキーワード「年利1.0%で複利運用」が重要になります。
この「年利1.0%で複利運用」という意味は毎年貯まったお金に1.0%の利息が付きますという意味です。
複利の考え方はここでは細かく理解する必要はなく毎年利息が付くというところが理解できれば問題ありません。
毎年利息が付くということは毎年貯めた金額に利息が付いているので以下の関係式が成り立ちます。
毎年積み立てるお金+積み立てたお金につく利息=100万円
よって毎年積み立てるお金は100万円より少なくて済むということです。
実際に2つの係数で計算してみましょう。
10,000,000×0.096=960,000
10,000,000×0.106=1,060,000
100万円より少なくて済むので960,000が正解となります。
係数だけで判断する場合利息が付くから1÷10倍(年数分)よりも小さい係数を使うということがわかれば2つ計算しなくても答えが出せます。
次に1÷年数より大きい係数についてですが以下のキーワードが出てきた時に使用します。
・〇年間で切り崩す(ローンの場合は〇年間支払う)
・毎年受け取る(ローンの場合は毎年支払う)
この場合問題に記載される金額は持っているお金(ローンの合計画)で切り崩す金額や毎年受け取る金額を求めることになります。
例えば1000万円のお金を10年間受取りたいとしましょう。
1000万円÷10年間=100万円となります。
ここで問題に必ず記載されているキーワード「年利1.0%で複利運用」が重要になります。
準備したお金は毎年減っていくわけですが残金に利息が付きます。
ということは毎年受け取れるお金は以下の関係式が成り立ちます。
毎年受け取れるお金×10年間=1000万円+残金の利息
よって10年間でもらえるお金は1000万円より多くなるということなので毎年もらえるお金は100万円より多くなります。
実際に2つの係数で計算してみましょう。
10,000,000×0.096=960,000
10,000,000×0.106=1,060,000
100万円より多くもらえるので1,060,000が正解となります。
係数だけで判断する場合利息が付くから1÷10倍(年数分)よりも大きい係数を使うということがわかれば2つ計算しなくても答えが出せます。
3.【裏ワザ】キーワードから使用する係数を求める
ここまで6つの係数の名前を覚えなくでも答えを出す方法を説明してきました。
最後にキーワードから使用する係数を求めるフローを【裏ワザ】として作成しましたので活用してみてください。
過去7回の試験での問題分に必ず似たようなキーワードが出てきています。
ローンの問題が出題された場合は毎年受け取るや切り崩すという言葉を毎年支払うに読み替えるとさらにわかりやすいです。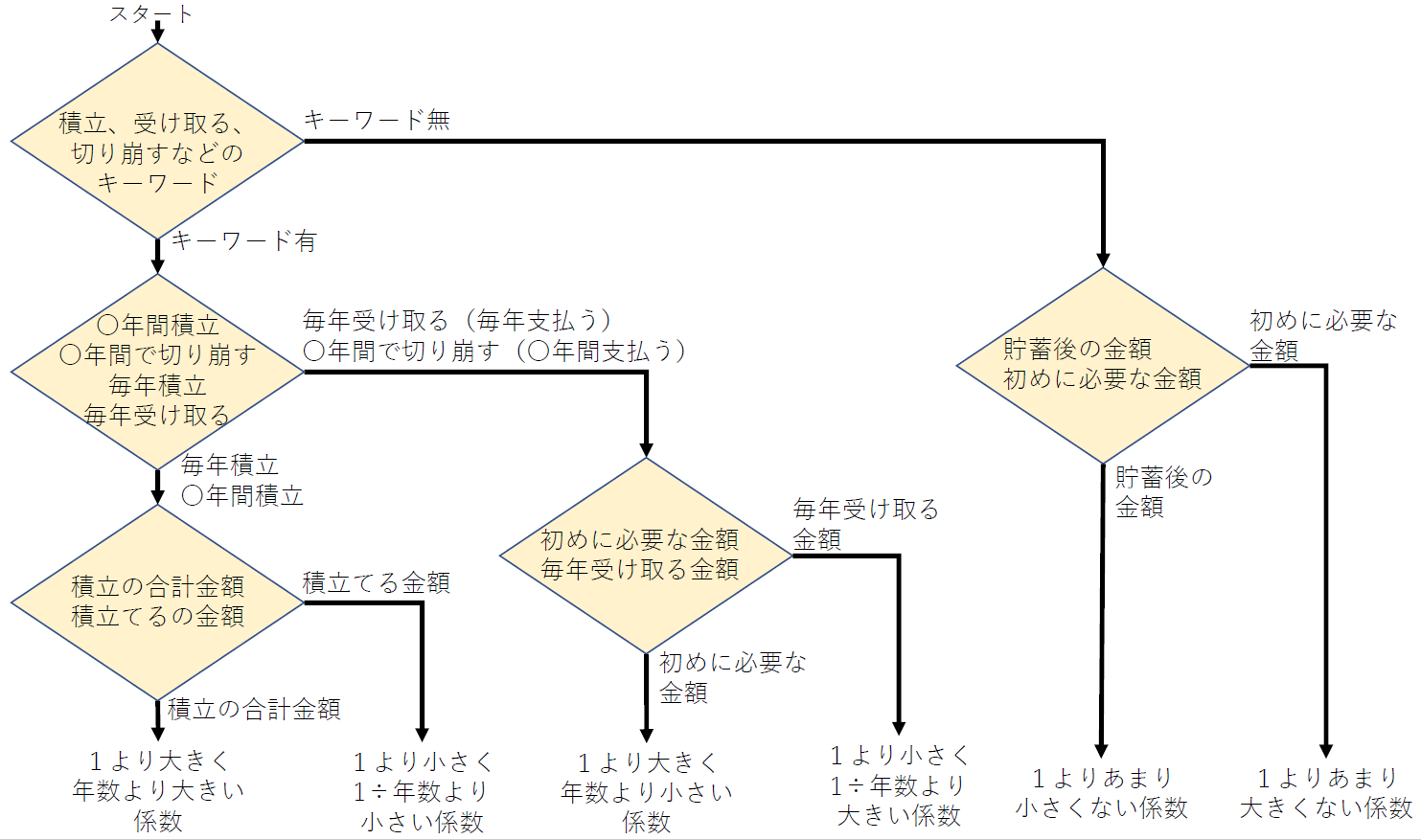
4.過去問解説
それでは過去問を使用して具体的にどのように解くか解説していきます。
ここではFP2級実技試験(資産設計提携業務)FP3級実技試験(資産設計提携業務)を用いて解説します。
2022年1月過去問
①2022/1 FP2級実技試験(資産設計提案業務)より
問26
榎田さんは、相続により受け取った400万円を運用しようと考えている。これを10年間、年利1.0%で複利運用した場合、10年後の合計額はいくらになるか。
【解説】
「400万円を運用しよう考えている」と書かれていますので増やすことを考えています。
よって1倍よりも大きい3つの係数に絞られます。
係数早見表
| 終価係数 | 年金終価係数 | 年金原価係数 | |
| 10年 | 1.105 | 10.462 | 9.471 |
次に「10年間、年利1.0%で複利運用した」と書かれていますので利息分しか増加しません。
この時点で「終価係数」を使用することがわかる人は問題ないですが「〇年間積み立て」「〇年間で切り崩す」という言葉と「毎年積立」「毎年受け取る」という言葉があるかないかで判断もできます。
この問題ではそれらの言葉がでてきていないため400万のお金は利息の分だけ増えないため額は少ないということがわかります。
この結果1倍よりも大きい係数の中で1からおまり大きくない係数になります。
4,000,000×1.105(10年の係数の中で1倍よりも大きくその中で1からおまり大きくない係数)=4,420,000
問27
鶴見さんは、老後の生活資金として、毎年年末に100万円を受け取りたいと考えている。受取期間を25年間とし、年利1.0%で複利運用をした場合、受取り開始年の初めにいくらの資金があればよいか。
【解説】
「毎年年末に100万円を受け取りたい」「受取期間を25年間」という2つのキーワードから最初用意する資金は100万円より多く必要なので係数は1倍よりも大きい係数を使用することがわかります。
ここで「毎年~受け取りたい」という言葉が出てきたので1倍よりも大きい係数の中の1からだいぶ大きい係数2つに絞られます。
係数早見表
| 終価係数 | 年金終価係数 | 年金原価係数 | |
| 25年 | 1.282 | 28.243 | 22.023 |
どちらを使用するか迷った場合は両方計算してしまいましょう。
1,000,000×28.243=28,243,000
1,000,000×22.023=22,023,000
「毎年年末に100万円を受け取りたい」「受取期間を25年間」ということなので100万×25年間=2500万円必要です。
そこで最後のキーワードとして「年利1.0%で複利運用」があります。
毎年お金を受け取るので減っていきますがその間も複利運用しているので残金に利息がつくためお金は増えていきます。
よって準備するお金は2500万円より少なくて済みます。
その結果2500万円より少ない金額の方が答えになります。
1,000,000×22.023=22,023,000
ここまでは両方計算しましたが実は係数を見ただけでどちらかわかります。
どの年の係数を見ても同じなんですが必ず年数よりも大きい方と小さいほうの係数になります。
25年の例でいうと
28.243>25>22.023
という関係です。
最初の解説では計算した金額で比較しましたが準備するお金が25年分=25倍よりも少ないお金を準備すればよいということがわかると使用する係数が22.023だということがわかります。
問28
伊丹さんは、将来の子どもの進学費用の準備として新たに積立てを開始する予定である。毎年年末に30万円を積み立てるものとし、8年間、年利1.0%で複利運用しながら積み立てた場合、8年後の合計額はいくらになるか。
【解説】
「毎年年末に30万円を積み立てる」「8年間」という2つのキーワードからお金を貯めているので係数は1倍よりも大きい係数を使用することがわかります。
ここで「毎年~積み立てる」という言葉が出てきたので1倍よりも大きい係数の中の1からだいぶ大きい係数2つに絞られます。
係数早見表
| 終価係数 | 年金終価係数 | 年金原価係数 | |
| 8年 | 1.083 | 8.286 | 7.652 |
どちらを使用するか迷った場合は両方計算しましょう。
300,000×8.286=2,485,800
300,000×7.652=2,295,600
ここで最後のキーワードとして「年利1.0%で複利運用」があります。
毎年お金を積み立てている間も複利分のお金が増えます。
よって、30万円を8年間積み立てた金額300,000×8=2,400,000よりも多い金額の方が答えになります。
300,000×8.286=2,485,800
ここまでは両方計算しましたが実は係数を見ただけでどちらかわかります。
どの年の係数を見ても同じなんですが必ず年数よりも大きい方と小さいほうの係数になります。
8年の例でいうと
8.286>8>7.652
という関係です。
最初の解説では計算した金額で比較しましたが積み立てたお金が8年分=8倍よりも多くなるということがわかると使用する係数が8.286だということがわかります。
②2022/1 FP3級実技試験(資産設計提案業務)より
問17
航平さんは、60歳で定年を迎えた後、公的年金の支給が始まる65歳までの5年間の生活資金に退職一時金の一部を充てようと考えている。仮に退職一時金のうち500万円を年利2.0%で複利運用しながら5年間で均等に取り崩すこととした場合、年間で取り崩すことができる最大金額として、正しいものはどれか。なお、下記<資料>の3つの係数の中から最も適切な係数を選択して計算し、円単位で解答すること。また、税金や記載のない事項については一切考慮しないこととする。
<資料:係数早見表(年利2.0%)>
*記載されている数値は正しいものとする。
1. 960,800円
2. 1,060,800円
3. 1,104,000円
【解説】
「退職一時金のうち500万円」「5年間で均等に取り崩す」「年間で取り崩すことができる最大金額」というキーワードからお金は500万から減る方向なので1よりも小さい係数を使用することがわかります。
残りの係数のどちらを使用したらよいか迷ったら両方計算しましょう。
5,000,000×0.21216=1,060,800
5,000,000×0.19216=960,800
ここで最後のキーワードとして「年利2.0%で複利運用」があります。
毎年お金を受け取るので減っていきますがその間も複利運用しているので残っているお金は増えていきます。
複利運用しないで500万を5年間毎年受け取る場合500万÷5年間=100万円になります。
今回は複利運用しているので毎年受け取る金額は100万より多くなります。
その結果100万円より多い金額の方が答えになります。
5,00,000×0.21216=1,060,800→正解は2
ここまでは両方計算しましたが実は係数を見ただけでどちらかわかります。
どの年数の係数を見ても同じなんですが1÷年数よりも大きい係数と小さい係数になります。
5年の例でいうと
0.21216>1÷5年=0.2>0.19216
という関係です。
最初の解説では計算した金額で比較しましたが切り崩すお金が5年分=1/5=0.2倍よりも多くなるということがわかると使用する係数が0.21216だということがわかります。
2021年9月過去問
①2021/9 FP2級実技試験(資産設計提案業務)より
問26
志田さんは、住宅のリフォーム費用として6年後に300万円を準備したいと考えている。6年間、年利1.0%で複利運用する場合、現在いくらの資金があればよいか。
【解説】
「6年後に300万円を準備したい」と書かれていますので求める金額を増やして300万にすることを考えています。
よって、300万>求める金額となりますので1倍よりも小さい3つの係数に絞られます。
係数早見表
| 現価係数 | 減債基金係数 | 資本回収係数 | |
| 6年 | 0.942 | 0.163 | 0.173 |
次に「6年間、年利1.0%で複利運用する」と書かれていますので利息分しか増加しません。
この時点で「現価係数」を使用することがわかる人は問題ないですが「〇年間積み立て」「〇年間で切り崩す」という言葉と「毎年積立」「毎年受け取る」という言葉があるかないかで判断もできます。
この問題ではそれらの言葉がでてきていないため目標額300万と求める金額は利息の分だけの差になります。
この結果1からあまり小さくない係数になります。
3,000,000×0.942(6年の係数の中で1倍よりも小さくその中で1からあまり小さくない係数)=2,826,000
問27
大久保さんは、自動車の購入費用200万円をマイカーローンを利用して返済しようと考えている。
今後6年間、年利1.0%で毎年借入応当日に元利均等返済をする場合、毎年の返済額はいくらになるか。
【解説】
「200万円をマイカーローンを利用して」「今後6年間、年利1.0%で毎年借入応当日に元利均等返済」と書かれていますので200万円のローンを6年間で返済することを考えています。
ここで「元利均等返済」という言葉が出てきていますが6つの係数を使用した問題の中でローンを返済する問題が出題された場合は必ず「元利均等返済」になりますのであまり言葉を気にする必要はありません。
「元利均等返済」にしないと複利で利息がつかないからです。
よって200万>求める金額となりますので1倍よりも小さい3つの係数に絞られます。
ここで「毎年~返済」という言葉が出てきたので1倍よりも小さい係数の中の1からだいぶ小さい係2つに絞られます。
係数早見表
| 現価係数 | 減債基金係数 | 資本回収係数 | |
| 6年 | 0.942 | 0.163 | 0.173 |
残りの係数のどちらを使用したらよいか迷ったら両方計算しましょう。
2,000,000×0.163=326,000
2,000,000×0.173=346,000
ここで最後のキーワードとして「年利1.0%で毎年借入応当日に元利均等返済」があります。
ローンの返済は残金に複利が付きます(毎年利息が付きます)のでローン金額(200万円)÷年数(6年間)=約33400円<毎年支払う金額という式が成り立ちます。
334,000よりも大きい金額が支払う金額が答えになります。
2,000,000×0.173=346,000
ここまでは両方計算しましたが実は係数を見ただけでどちらかわかります。
どの年数の係数を見ても同じなんですが1÷年数よりも大きい係数と小さい係数になります。
6年の例でいうと
0.173>1÷6年=0.166・・・>0.163
という関係です。
最初の解説では計算した金額で比較しましたが切り崩すお金が6年分=1/6=0.166倍よりも多くなるということがわかると使用する係数が0.173だということがわかります。
問28
沼田さんは、子の教育資金として、10年後に500万円を用意しようと考えている。年利1.0%で複利運用しながら毎年年末に一定額を積み立てる場合、毎年いくらずつ積み立てればよいか。
【解説】
「10年後に500万円を用意しよう」「毎年年末に一定額を積み立てる」という2つのキーワードから求める金額を毎年積み立てて500万にすることを考えています。
よって、500万>求める積み立て金額となりますので1倍よりも小さい3つの係数に絞られます。
ここで「毎年~積み立てる」という言葉が出てきたので1倍よりも小さい係数の中の1からだいぶ小さい係数が2つに絞られます。
係数早見表
| 現価係数 | 減債基金係数 | 資本回収係数 | |
| 10年 | 0.905 | 0.096 | 0.106 |
どちらを使用するか迷った場合は、両方計算しましょう。
5,000,000×0.096=480,000
5,000,000×0.106=530,000
ここで最後のキーワードとして「年利1.0%で複利運用」があります。
毎年お金を積み立てている間も複利分のお金が増えます。
よって500万円を10年間積み立てる金額5,000,000÷10=500,000よりも少ない金額の方が答えになります。
5,000,000×0.096=480,000
ここまでは両方計算しましたが実は係数を見ただけでどちらかわかります。
どの年数の係数を見ても同じなんですが1÷年数よりも大きい係数と小さい係数になります。
10年の例でいうと
0.106>1÷10年=0.1>0.096
という関係です。
最初の解説では計算した金額で比較しましたが毎年積み立てるお金が10年分=1/10=0.1倍よりも少なくなるということがわかると使用する係数が0.096だということがわかります。
②2021/9 FP3級実技試験(資産設計提案業務)より
問17
大地さんは、今後10年間で積立貯蓄をして、老後の資金として350万円を準備したいと考えている。積立期間中に年利2.0%で複利運用できるものとした場合、350万円を準備するために必要な毎年の積立金額として、正しいものはどれか。なお、下記<資料>の3つの係数の中から最も適切な係数を選択して計算し、解答に当たっては、千円未満を切り上げること。また、税金や記載のない事項については一切考慮しないこととする。
<資料:係数早見表(年利2.0%)>

*記載されている数値は正しいものとする。
1. 288,000円
2. 320,000円
3. 390,000円
【解説】
「10年間で積立貯蓄」「350万円を準備したい」というキーワードから求める金額を毎年積み立てて350万にすることを考えています。
よって350万>求める積み立て金額となりますので1倍よりも小さい3つの係数に絞られます。
ここで「毎年の積立金額」という言葉が出てきたので1倍よりも小さい係数の中の1からだいぶ小さい係数が2つに絞られます。
係数早見表
| 現価係数 | 資本回収係数 | 減債基金係数 | |
| 10年 | 0.82035 | 0.11133 | 0.09133 |
残りの係数のどちらを使用したらよいか迷ったら両方計算しましょう。
3,500,000×0.11133=389,655→千円未満切り上げ→390,000
3,500,000×0.09133=319,655→千円未満切り上げ→320,000
ここで最後のキーワードとして「年利2.0%で複利運用」があります。
毎年お金を積み立てている間も複利運用しているので積み立てているお金は増えていきます。
複利運用しないで350万を10年間で貯める場合350万÷10年間=35万円になります。
今回は複利運用しているので毎年貯まる金額は35万より多くなります。
その結果35万円より少ない金額を貯蓄すればよいので35万円より少ないの方が答えになります。
3,500,000×0.09133=319,655→千円未満切り上げ→320,000→正解は2
ここまでは両方計算しましたが実は係数を見ただけでどちらかわかります。
どの年数の係数を見ても同じなんですが1÷年数よりも大きい係数と小さい係数になります。
10年の例でいうと
0.11133>1÷10年=0.1>0.09133
という関係です。
最初の解説では計算した金額で比較しましたが積み立てるお金が10年分=1/10=0.1倍よりも少なくて済むということがわかると使用する係数が0.09133だということがわかります。
5.まとめ
6つの係数の名前を覚えずに問題のキーワードを用いて計算する方法を説明しました。
実技試験では点数を必ずとれる問題ですので活用してみてください。
【裏ワザ】としてキーワードのフローもありますので是非活用してみてください!
